module_approx.mws
Informatique
Approximation
Le but de ce chapitre est de présenter une réalisation en
Maple
des différents algorithmes d'approximation figurant au programme. On pourra se reporter au polycopié correspondant.
I. Méthode du point fixe
Pour calculer le(s) point(s) fixe(s) d'une fonction
f
, on utilise une suite récurrente définie par la donnée de
![x[0]](graphics/module_approx1.gif) dans
R
et la relation de récurrence
dans
R
et la relation de récurrence
![x[n+1] = f(x[n])](graphics/module_approx2.gif) .
.
On rappelle que si
f
est
contractante
(càd,
k
-lipschitzienne avec une constante
k<
1), l'écart entre
![x[n]](graphics/module_approx3.gif) et le point fixe
et le point fixe
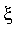 (alors unique) de
f
est majoré par
(alors unique) de
f
est majoré par
![abs(x[n]-xi) < k^n/(1-k)](graphics/module_approx5.gif) .
.
![abs(x[1]-x[0])](graphics/module_approx6.gif) .
.
1.
Écrire une procédure
pointFixe
prenant pour arguments
f
,
![x[0]](graphics/module_approx7.gif) ,
k
et la
précision
souhaitée, et retournant une valeur approchée de
,
k
et la
précision
souhaitée, et retournant une valeur approchée de
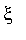 à la précision demandée.
à la précision demandée.
2.
Lorsque
f
est la fonction
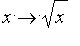 sur [
sur [
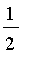 ,2], donner une estimation de
k
et vérifier que la procédure précédente fournit bien une valeur approchée de
,2], donner une estimation de
k
et vérifier que la procédure précédente fournit bien une valeur approchée de
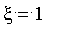 à
à
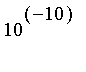 près.
près.
II. Méthode de dichotomie
On cherche ici une valeur approchée d'une solution de l'équation "
f
(
x
)=0", où
f
est une fonction continue sur [
a
,
b
] avec
f
(
a
) et
f
(
b
) de signes contraires.
On définit deux suites (
![x[n]](graphics/module_approx13.gif) ) et (
) et (
![y[n]](graphics/module_approx14.gif) ) en posant
) en posant
![x[0] = a](graphics/module_approx15.gif) ,
,
![y[0] = b](graphics/module_approx16.gif) et de proche en proche :
et de proche en proche :
-
si
![f((x[n]+y[n])/2)](graphics/module_approx17.gif) a le même signe que
a le même signe que
![f(x[n])](graphics/module_approx18.gif) :
:
![x[n+1] = (x[n]+y[n])/2](graphics/module_approx19.gif) et
et
![y[n+1] = y[n]](graphics/module_approx20.gif) ;
;
-
si
![f((x[n]+y[n])/2)](graphics/module_approx21.gif) a le même signe que
a le même signe que
![f(y[n])](graphics/module_approx22.gif) :
:
![x[n+1] = x[n]](graphics/module_approx23.gif) et
et
![y[n+1] = (x[n]+y[n])/2](graphics/module_approx24.gif) .
.
On vérifie alors que les suites (
![x[n]](graphics/module_approx25.gif) ) et (
) et (
![y[n]](graphics/module_approx26.gif) ) sont adjacentes, convergentes vers une solution
) sont adjacentes, convergentes vers une solution
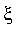 de l'équation "
f
(
x
)=0", et que l'errreur commise en remplaçant
de l'équation "
f
(
x
)=0", et que l'errreur commise en remplaçant
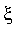 par
par
![x[n]](graphics/module_approx29.gif) (
resp.
(
resp.
![y[n]](graphics/module_approx30.gif) ) est majorée par
) est majorée par
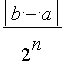 .
.
1.
Écrire une procédure
dicho
prenant pour arguments
f
,
a
,
b
et la précision souhaitée, et retournant une valeur approché de
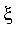 à la précision demandée.
à la précision demandée.
2.
Lorsque
f
est la fonction
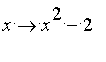 , utiliser la procédure précédente pour calculer une valeur approchée de
, utiliser la procédure précédente pour calculer une valeur approchée de
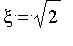 à
à
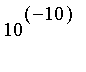 près.
près.
III. Méthode de Newton
On rappelle que cette méthode permet de calculer de manière approchée la solution
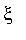 d'une équation
d'une équation
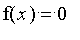
en itérant la suite définie par le choix de
![x[0]](graphics/module_approx38.gif) (>
(>
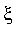 ) et la relation de récurrence
) et la relation de récurrence
![x[n+1] = x[n]-f(x[n])/D(f)(x[n])](graphics/module_approx40.gif) ,
,
L'erreur commise est contrôlée par
![abs(x[n]-xi) <= 2*m[1]/M[2]](graphics/module_approx41.gif) .
.
![(M[2]/(2*m[1])*(x[0]-a))^(2^n)](graphics/module_approx42.gif) ,
,
où
![m[1]](graphics/module_approx43.gif) (
resp.
(
resp.
![M[2]](graphics/module_approx44.gif) ) est un minorant (
resp
majorant) de
f'
(
resp. f''
) sur [
a
,+
) est un minorant (
resp
majorant) de
f'
(
resp. f''
) sur [
a
,+
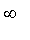 [ (
a
désignant une valeur <
[ (
a
désignant une valeur <
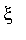 supposée connue).
supposée connue).
1.
Écrire une procédure
Newton
dont les arguments sont
f
,
a
,
![x[0]](graphics/module_approx47.gif) ,
,
![m[1]](graphics/module_approx48.gif) ,
,
![M[2]](graphics/module_approx49.gif) , et la précision de l'approximation cherchée, et retournant une valeur
, et la précision de l'approximation cherchée, et retournant une valeur
![x[n]](graphics/module_approx50.gif) convenablement proche de
convenablement proche de
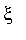 .
.
2.
On applique cette procédure à la fonction
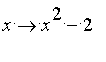 (donc :
(donc :
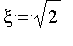 ).
).
(a)
Constater que les valeurs suivantes conviennent :
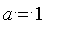 ,
,
![x[0] = 2](graphics/module_approx55.gif) ,
,
![m[1] = 2](graphics/module_approx56.gif) ,
,
![M[2] = 2](graphics/module_approx57.gif) .
.
(b)
Utiliser la procédure
Newton
pour calculer une valeur approchée de
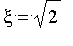 à
à
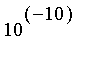 près.
près.
IV. Algorithme de Héron
L'algorithme de Héron d'Alexandrie permet depuis plus de vingt siècle de calculer des valeurs approchées de la racine carrée d'un reél positif
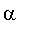 . Il repose sur l'itération de la suite (
. Il repose sur l'itération de la suite (
![x[n]](graphics/module_approx61.gif) ) définie par la donnée de
) définie par la donnée de
![x[0]](graphics/module_approx62.gif) >
>
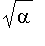 (max(
(max(
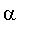 ,1) convient) et la relation de récurrence :
,1) convient) et la relation de récurrence :
![x[n+1] = 1/2](graphics/module_approx65.gif) .(
.(
![x[n]+alpha/x[n]](graphics/module_approx66.gif) ).
).
L'erreur est majorée par
![2*sqrt(alpha)*(epsilon[0]/(2*sqrt(alpha)))^(2^n)](graphics/module_approx67.gif) ,
,
où
![epsilon[0] = x[0]-alpha](graphics/module_approx68.gif) .
.
1.
Écrire une procédure
Heron
prenant pour arguments
a
(<
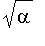 ),
),
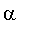 ,
,
![x[0]](graphics/module_approx71.gif) et la précision souhaitée, et retournant une approximation de
et la précision souhaitée, et retournant une approximation de
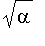 de la précision demandée.
de la précision demandée.
2.
Lorsque
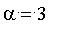 et
et
![x[0] = 2](graphics/module_approx74.gif) , constater que
, constater que
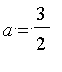 convient et utiliser la procédure précédente pour calculer une valeur approchée de
convient et utiliser la procédure précédente pour calculer une valeur approchée de
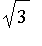 à
à
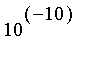 près.
près.
V. Calcul approché de
e
e
est par définition la limite de la suite (
![x[n]](graphics/module_approx78.gif) ) définie par :
) définie par :
(1)
![x[n] = Sum(1/k!,k = 0 .. n)](graphics/module_approx79.gif) .
.
Mais si d'autre part
![y[n] = x[n]+1/(n*n!)](graphics/module_approx80.gif) , (avec
, (avec
![y[0] = 4](graphics/module_approx81.gif) ), on montre que (
), on montre que (
![x[n]](graphics/module_approx82.gif) ) et (
) et (
![y[n]](graphics/module_approx83.gif) ) sont adjacentes et encadrent
e
avec une erreur ne dépassant pas
) sont adjacentes et encadrent
e
avec une erreur ne dépassant pas
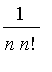 .
.
1.
Écrire une procédure
E
prenant un seul argument, la précision demandée, et retournant une approximation de
e
avec cette précision.
Dans le souci de ne faire aucun calcul inutile, on évitera de faire appel à la fonction factorielle. On utilisera plutôt un calcul de proche en proche.
2.
Utiliser cette procédure pour obtenir une approximation de
e
à
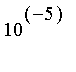 près.
près.
3.
Quel problème présente cette procédure ? Comment pourrait-on le résoudre ?
VI. Méthode d'Archimède
Rappelons que la méthode d'Archimède pour le calcul de
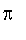 consiste à encadrer ce dernier par deux suites (
consiste à encadrer ce dernier par deux suites (
![p[n]](graphics/module_approx87.gif) ) et (
) et (
![q[n]](graphics/module_approx88.gif) ) définies par
) définies par
![c[0] = 1/2](graphics/module_approx89.gif) ,
,
![p[0] = 3*sqrt(3)/2](graphics/module_approx90.gif) , les relations de récurrence
, les relations de récurrence
![c[n+1] = sqrt((1+c[n])/2)](graphics/module_approx91.gif) et
et
![p[n+1] = p[n]/c[n+1]](graphics/module_approx92.gif) ,
,
et enfin
![q[n] = p[n]/c[n]](graphics/module_approx93.gif) .
.
L'erreur commise ne dépasse pas
![q[n]-p[n] = p[n]*(1/c[n]-1)](graphics/module_approx94.gif) , expression qui ne se simplifie pas favorablement et que l'on recalculera à chaque étape.
, expression qui ne se simplifie pas favorablement et que l'on recalculera à chaque étape.
1.
Écrire une procédure
Archimede
prenant comme unique argument la précision demandée, et retournant une valeur approchée de
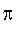 correspondant à cette précision.
correspondant à cette précision.
2.
Grâce à cette procédure, calculer une valeur approchée de
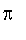 à
à
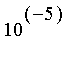 près.
près.
VII. Formule d'Euler
On peut aussi approximer
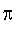 en utilisant les formules en arctan inventées par Euler au XVIIIème siècle. Par exemple
en utilisant les formules en arctan inventées par Euler au XVIIIème siècle. Par exemple
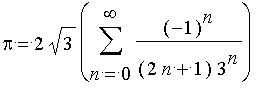 .
.
Si l'on arrête la somme à l'indice
N
, l'erreur commise est majorée par
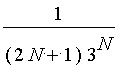 .
.
1.
Écrire une procédure
Euler
prenant comme unique argument la précision cherchée et calculant les termes de la somme précédente jusqu'à ce que l'erreur devienne inférieure à la précision demandée.
Dans un souci d'élégance et d'efficacité, on n'effectuera pas d'élévation à la puissance, mais seulement des multiplications, pour calculer les puissances de 3 de proche en proche, et ceci aussi bien pour le calcul de la somme que pour l'estimation de l'erreur.
2.
Calculer grâce à la procédure précédente une valeur approchée de
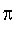 à
à
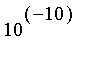 près.
près.
VIII. Formule des trapèzes
Rappelons qu'une intégrale
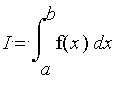 peut être approximée à l'aide des sommes :
peut être approximée à l'aide des sommes :
![I[n] = h*Sum((f(x[k])+f(x[k+1]))/2,k = 0 .. n-1)](graphics/module_approx104.gif) , (formule des trapèzes)
, (formule des trapèzes)
avec
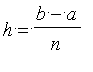 et
et
![x[k] = a+k*h](graphics/module_approx106.gif) . L'erreur est majorée par
. L'erreur est majorée par
![abs(I-I[n]) <= (b-a)^3*M[2]/(12*n^2)](graphics/module_approx107.gif) (où
(où
![M[2] = abs(abs(`f](graphics/module_approx108.gif) ), mais on a intérêt à calculer directement
), mais on a intérêt à calculer directement
![I[2^p]](graphics/module_approx109.gif) qui contient déjà tous les termes de
qui contient déjà tous les termes de
![I[2^(p-1)]](graphics/module_approx110.gif) .
.
1.
Écrire une procédure
trapeze
prenant cinq arguments : la fonction
f
,
a
,
b
(avec
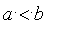 ),
),
![M[2]](graphics/module_approx112.gif) et la précision demandée, et effectuant le calcul de proche en proche des
et la précision demandée, et effectuant le calcul de proche en proche des
![I[2^p]](graphics/module_approx113.gif) (en tirant parti de la remarque précédente) jusqu'à ce que l'erreur devienne inférieure à la précision souhaitée.
(en tirant parti de la remarque précédente) jusqu'à ce que l'erreur devienne inférieure à la précision souhaitée.
2.
On s'intéresse à la fonction
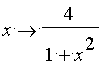 , pour laquelle l'intégrale de
, pour laquelle l'intégrale de
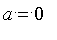 à
à
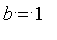 est facile à calculer et vaut
est facile à calculer et vaut
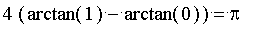 .
.
(a)
En étudiant
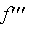 à l'aide de
Maple
, déterminer
à l'aide de
Maple
, déterminer
![M[2] = abs(abs(`f](graphics/module_approx119.gif) .
.
(b)
Utiliser alors la procédure
trapeze
pour obtenir une valeur approchée de
I
à
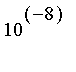 près.
près.
![]() dans
R
et la relation de récurrence
dans
R
et la relation de récurrence
![]() .
.
![]() et le point fixe
et le point fixe
![]() (alors unique) de
f
est majoré par
(alors unique) de
f
est majoré par
![abs(x[n]-xi) < k^n/(1-k)](graphics/module_approx5.gif) .
.
![]() .
.
![]() ,
k
et la
précision
souhaitée, et retournant une valeur approchée de
,
k
et la
précision
souhaitée, et retournant une valeur approchée de
![]() à la précision demandée.
à la précision demandée.
![]() sur [
sur [
![]() ,2], donner une estimation de
k
et vérifier que la procédure précédente fournit bien une valeur approchée de
,2], donner une estimation de
k
et vérifier que la procédure précédente fournit bien une valeur approchée de
![]() à
à
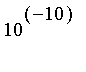 près.
près.
![f((x[n]+y[n])/2)](graphics/module_approx17.gif) a le même signe que
a le même signe que
![x[n+1] = (x[n]+y[n])/2](graphics/module_approx19.gif) et
et
![f((x[n]+y[n])/2)](graphics/module_approx21.gif) a le même signe que
a le même signe que
![y[n+1] = (x[n]+y[n])/2](graphics/module_approx24.gif) .
.
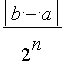 .
.
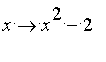 , utiliser la procédure précédente pour calculer une valeur approchée de
, utiliser la procédure précédente pour calculer une valeur approchée de
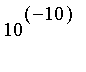 près.
près.
![x[n+1] = x[n]-f(x[n])/D(f)(x[n])](graphics/module_approx40.gif) ,
,
![abs(x[n]-xi) <= 2*m[1]/M[2]](graphics/module_approx41.gif) .
.
![(M[2]/(2*m[1])*(x[0]-a))^(2^n)](graphics/module_approx42.gif) ,
,
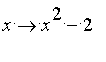 (donc :
(donc :
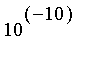 près.
près.
![x[n+1] = 1/2](graphics/module_approx65.gif) .(
.(
![x[n]+alpha/x[n]](graphics/module_approx66.gif) ).
).
![2*sqrt(alpha)*(epsilon[0]/(2*sqrt(alpha)))^(2^n)](graphics/module_approx67.gif) ,
,
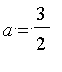 convient et utiliser la procédure précédente pour calculer une valeur approchée de
convient et utiliser la procédure précédente pour calculer une valeur approchée de
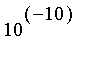 près.
près.
![x[n] = Sum(1/k!,k = 0 .. n)](graphics/module_approx79.gif) .
.
![y[n] = x[n]+1/(n*n!)](graphics/module_approx80.gif) , (avec
, (avec
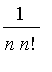 .
.
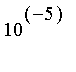 près.
près.
![c[0] = 1/2](graphics/module_approx89.gif) ,
,
![p[0] = 3*sqrt(3)/2](graphics/module_approx90.gif) , les relations de récurrence
, les relations de récurrence
![c[n+1] = sqrt((1+c[n])/2)](graphics/module_approx91.gif) et
et
![p[n+1] = p[n]/c[n+1]](graphics/module_approx92.gif) ,
,
![q[n] = p[n]/c[n]](graphics/module_approx93.gif) .
.
![q[n]-p[n] = p[n]*(1/c[n]-1)](graphics/module_approx94.gif) , expression qui ne se simplifie pas favorablement et que l'on recalculera à chaque étape.
, expression qui ne se simplifie pas favorablement et que l'on recalculera à chaque étape.
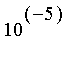 près.
près.
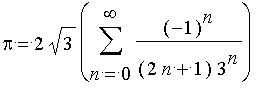 .
.
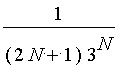 .
.
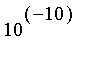 près.
près.
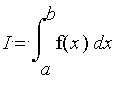 peut être approximée à l'aide des sommes :
peut être approximée à l'aide des sommes :
![I[n] = h*Sum((f(x[k])+f(x[k+1]))/2,k = 0 .. n-1)](graphics/module_approx104.gif) , (formule des trapèzes)
, (formule des trapèzes)
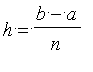 et
et
![abs(I-I[n]) <= (b-a)^3*M[2]/(12*n^2)](graphics/module_approx107.gif) (où
(où
![I[2^(p-1)]](graphics/module_approx110.gif) .
.
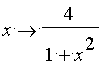 , pour laquelle l'intégrale de
, pour laquelle l'intégrale de
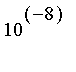 près.
près.