Tracés en coordonnées cartésiennes
1.
Regarder
l'aide sur plot
, en particulier les
exemples
, pour voir comment tracer en
Maple
une courbe paramétrée donnée sous la forme
![]() ,
,
![]() .
.
2. On va détailler grâce à Maple l'étude de l'arc paramétré suivant :
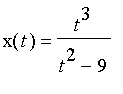 ;
;
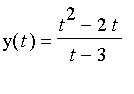
(a)
Faites-la tracer par
Maple
(en faisant décrire à
t
un intervalle convenable --
pas
]
![]() ,+
,+
![]() [ !). Il est normal d'avoir à effectuer plusieurs essais, notamment pour obtenir un aspect satisfaisant pour les branches infinies. Il ne suffit pas de spécifier l'intervalle de variation de
t
, il faut en outre imposer des bornes convenables à l'abscisse et à l'ordonnée.
[ !). Il est normal d'avoir à effectuer plusieurs essais, notamment pour obtenir un aspect satisfaisant pour les branches infinies. Il ne suffit pas de spécifier l'intervalle de variation de
t
, il faut en outre imposer des bornes convenables à l'abscisse et à l'ordonnée.
| > |
| > |
(b)
Étude de la branche infinie pour
![]() . Déterminer à l'aide de
Maple
les limites
. Déterminer à l'aide de
Maple
les limites
![]() de
de
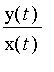 puis
puis
![]() de
de
![]() . Définir l'équation de l'asymptote
. Définir l'équation de l'asymptote
![]() obtenue.
obtenue.
| > |
| > |
| > |
(c)
Étude de la branche infinie pour
![]() . Déterminer à l'aide de
Maple
les limites
. Déterminer à l'aide de
Maple
les limites
![]() de
de
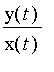 puis
puis
![]() de
de
![]() . Définir l'équation de l'asymptote
. Définir l'équation de l'asymptote
![]() obtenue.
obtenue.
| > |
| > |
| > |
(d) À l'aide de l'instruction display de la bibliothèque plots , tracer sur un même schéma (et en couleurs différentes) la courbe et ses deux asymptotes.
| > | with(plots): |
| > |
| > |
| > |
3. Autre exemple au choix : reprendre avec l'aide de Maple l'étude d'une autre courbe paramétrée, sans oublier les branches infinies.
| > |
| > |
| > |
| > |
| > |
| > |
| > |
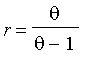 . Que dire du résultat ? Voir la
commande view
pour obtenir une représentation plus raisonnable. Comme au
I.
, confirmer à l'aide de
Maple
la nature des branches infinies.
. Que dire du résultat ? Voir la
commande view
pour obtenir une représentation plus raisonnable. Comme au
I.
, confirmer à l'aide de
Maple
la nature des branches infinies.
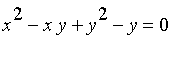 .
.
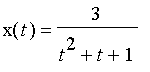 ;
;
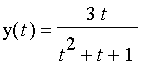 .
.