I. Découverte de
Maple
A ce niveau, vous êtes connecté au réseau et vous disposez d'un volume personnel (
K:
) et d'un volume en lecture seule (
H:
) depuis lequel vous avez ouvert ce fichier.
Enregistrez-en une copie dans votre volume personnel
K:
(
File - Save As
), sinon vous ne pourrez pas le modifier.
Les calculs que vous aurez à effectuer peuvent être faits
-
dans une feuille indépendante (que vous aurez créée par
File - New
) -- n'oubliez pas de l'enregistrer en lui donnant un nom --,
-
ou bien directement dans le fichier actuel (après que vous l'ayez transporté dans
K:
)
Ouvrez maintenant la présentation de
Maple
. Il vous suffit de cliquer sur le lien ci-dessous.
Vous devrez ensuite revenir à ce document grâce au menu
File - Open
.
Dans la présentation, consultez les sections (1) puis (11) (obligatoirement) puis (2) à (4) et (6) (éventuellement) pour voir comment
Maple
permet d'effectuer diverses sortes de calculs. Le fichier de présentation contient des exemples que vous pouvez exécuter : placez-vous sur l'un d'eux et appuyez sur
Entrée
.
En quittant ce fichier, bien sûr, vous ne tenterez pas d'enregistrer les modifications que vous y avez apportées.
Ouvrir la présentation.
II. Premiers calculs
Vous pouvez fermer, si ce n'est pas déjà fait, le fichier de présentation que vous étiez en train de consulter.
Effectuez maintenant les exemples de calculs suivants en
Maple
:
-
1+1
(c'est un début...) ;
-
décomposition de 60 en facteurs premiers (*) ;
-
valeur approchée de
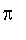 à
à
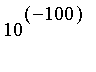 près ;
près ;
-
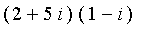 (attention à la notation du
i
en
Maple
!) ;
(attention à la notation du
i
en
Maple
!) ;
-
dérivée (*) cinquième de
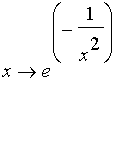 ; factorisez-la (*).
; factorisez-la (*).
(*) Pour chaque notion inconnue, essayez de trouver dans l'aide (
Help - Contents
) la commande correspondante.
Un exemple d'
édition
maintenant : supposons que vous ayez besoin de réutiliser le polynôme qui apparaît dans le dernier résultat, pour un calcul ultérieur. Pour cela sélectionnez-le : placez le curseur devant son premier terme et faites glisser (càd, déplacez la souris sans relâcher le bouton) jusqu'au dernier terme (inclus). Les termes "sélectionnés'' apparaissent en couleur différente. Choisissez alors "copier'' (
Edit - Copy
ou
Ctrl+C
ou
 "bouton'') puis placez le curseur à l'endroit où vous souhaitez retrouver ces termes. Choisissez enfin "coller'' (
Edit - Paste
ou
Ctrl+V
ou
"bouton'') puis placez le curseur à l'endroit où vous souhaitez retrouver ces termes. Choisissez enfin "coller'' (
Edit - Paste
ou
Ctrl+V
ou
 bouton) et ils réapparaissent à la bonne place. Vous pouvez ensuite réutiliser cette expression pour de nouveaux calculs.
bouton) et ils réapparaissent à la bonne place. Vous pouvez ensuite réutiliser cette expression pour de nouveaux calculs.
Les calculs suivants ont lieu dans
C
:
(a) Calcul de module et d'argument
Soit le complexe
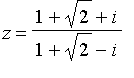 . Définissez-le en
Maple
. Calculez son module. Calculez son argument.
. Définissez-le en
Maple
. Calculez son module. Calculez son argument.
Il est nécessaire de le transformer avec
evalc
et
simplify
pour obtenir un résultat satisfaisant, et vous constaterez que l'ordre dans lequel on utilise ces fonctions n'est pas indifférent.
(b) Fonctions "problématiques"
i.
Qu'indique
Maple
si l'on demande une racine carrée du complexe
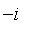 ? Comparez
? Comparez
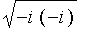 et
et
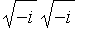 .
.
ii.
Qu'indique
Maple
si l'on demande un logarithme complexe de
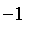 ? Comparez
? Comparez
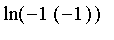 et
et
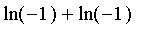 .
.
iii.
Que répond
Maple
si l'on calcule
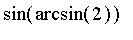 ? Que vaut, selon
Maple
,
? Que vaut, selon
Maple
,
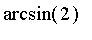 (alors que cette dernière valeur n'est normalement pas définie) ? Expliquez ce résultat en revenant à la définition du sinus à l'aide de l'exponentielle complexe.
(alors que cette dernière valeur n'est normalement pas définie) ? Expliquez ce résultat en revenant à la définition du sinus à l'aide de l'exponentielle complexe.
III. Etude d'une fonction
1.
Définissez en Maple la fonction
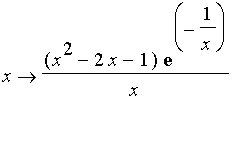 (Il s'agit d'une affectation à la variable f, de la forme :
f:= x->
(l'équivalent
Maple
de l'expression définissant
(Il s'agit d'une affectation à la variable f, de la forme :
f:= x->
(l'équivalent
Maple
de l'expression définissant
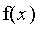 ).
).
2.
Testez une ou deux valeurs pour voir si ça marche bien (
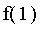 ,
,
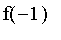 ,...).
,...).
3.
Même si celui-ci est ici évident,
Maple
permet-il de déterminer le domaine de définition de f ? (En anglais, les points n'appartenant pas au domaine de définition d'une fonction sont dits points singuliers --
singular
).
4.
Regardez les limites de f aux bornes de son domaine de définition :
(a) En +
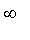 et
et
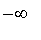 (comment cela s'appelle-t-il en
Maple
?)
(comment cela s'appelle-t-il en
Maple
?)
(b) En 0, de manière à prolonger éventuellement la fonction par continuité en ce point en posant
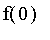 = ... ? Il faudra éventuellement distinguer les limites à droite et à gauche en 0.
= ... ? Il faudra éventuellement distinguer les limites à droite et à gauche en 0.
5.
(a) Calculez ensuite la dérivée de f. Il sera pratique de lui donner un nom (g p. ex.). Simplifiez l'expression obtenue. Celle-ci contient manifestement
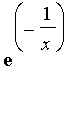 en facteur. Pour une subtile raison,
Maple
ne sait pas déterminer directement le signe d'une telle expression (non rationnelle).
en facteur. Pour une subtile raison,
Maple
ne sait pas déterminer directement le signe d'une telle expression (non rationnelle).
(b) Débarrassez-vous du facteur
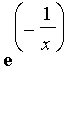 gênant en multipliant par
gênant en multipliant par
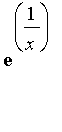 (fonction h). Cela ne modifie pas le signe. Factorisez l'expression rationnelle h.
(fonction h). Cela ne modifie pas le signe. Factorisez l'expression rationnelle h.
(c) Déterminez son signe en résolvant la condition "
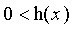 " par rapport à
x
. On connaît maintenant les variations de f.
" par rapport à
x
. On connaît maintenant les variations de f.
6.
On cherche ensuite à préciser la nature des branches infinies de f pour
x
®
±
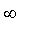 . Selon la méthode habituelle :
. Selon la méthode habituelle :
(a) Déterminez la limite éventuelle
a
de
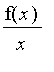 en ±
en ±
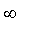 .
.
(b) Déterminez la limite éventuelle
b
de
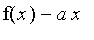 en ±
en ±
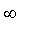 et interprétez géométriquement ces résultats.
et interprétez géométriquement ces résultats.
7.
Il reste encore à préciser "comment" se présente la courbe au voisinage du point que l'on a rajouté (image du paramètre
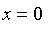 ). Trouvez un calcul approprié à cette étude, effectuez-le et concluez géométriquement.
). Trouvez un calcul approprié à cette étude, effectuez-le et concluez géométriquement.
8.
Pour confirmer les différentes études effectuées, représentez graphiquement sur un même schéma la courbe représentative de f et ses asymptotes éventuelles.
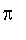 à
à
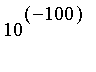 près ;
près ;
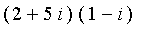 (attention à la notation du
i
en
Maple
!) ;
(attention à la notation du
i
en
Maple
!) ;
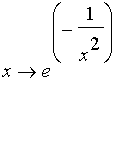 ; factorisez-la (*).
; factorisez-la (*).
 "bouton'') puis placez le curseur à l'endroit où vous souhaitez retrouver ces termes. Choisissez enfin "coller'' (
Edit - Paste
ou
Ctrl+V
ou
"bouton'') puis placez le curseur à l'endroit où vous souhaitez retrouver ces termes. Choisissez enfin "coller'' (
Edit - Paste
ou
Ctrl+V
ou
 bouton) et ils réapparaissent à la bonne place. Vous pouvez ensuite réutiliser cette expression pour de nouveaux calculs.
bouton) et ils réapparaissent à la bonne place. Vous pouvez ensuite réutiliser cette expression pour de nouveaux calculs.
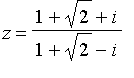 . Définissez-le en
Maple
. Calculez son module. Calculez son argument.
. Définissez-le en
Maple
. Calculez son module. Calculez son argument.
![]() ? Comparez
? Comparez
![]() et
et
![]() .
.
![]() ? Comparez
? Comparez
![]() et
et
![]() .
.
![]() ? Que vaut, selon
Maple
,
? Que vaut, selon
Maple
,
![]() (alors que cette dernière valeur n'est normalement pas définie) ? Expliquez ce résultat en revenant à la définition du sinus à l'aide de l'exponentielle complexe.
(alors que cette dernière valeur n'est normalement pas définie) ? Expliquez ce résultat en revenant à la définition du sinus à l'aide de l'exponentielle complexe.
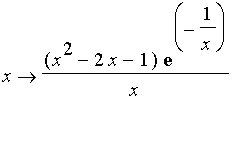 (Il s'agit d'une affectation à la variable f, de la forme :
f:= x->
(l'équivalent
Maple
de l'expression définissant
(Il s'agit d'une affectation à la variable f, de la forme :
f:= x->
(l'équivalent
Maple
de l'expression définissant
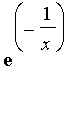 en facteur. Pour une subtile raison,
Maple
ne sait pas déterminer directement le signe d'une telle expression (non rationnelle).
en facteur. Pour une subtile raison,
Maple
ne sait pas déterminer directement le signe d'une telle expression (non rationnelle).
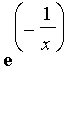 gênant en multipliant par
gênant en multipliant par
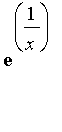 (fonction h). Cela ne modifie pas le signe. Factorisez l'expression rationnelle h.
(fonction h). Cela ne modifie pas le signe. Factorisez l'expression rationnelle h.
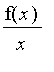 en ±
en ±