I.  Matrices - manipulations élémentaires

Le package linalg  ( lin ear alg ebra) sera bien utile pour effectuer toutes sortes d'opérations matricielles :

>	with(linalg):

1.  Voir l' aide sur matrix  pour la représentation d'une matrice (carrée ou non) en Maple . Définir deux matrices carrées 2x2 quelconques.

>

>

2.   Maple  sait multiplier les matrices, mais selon une syntaxe particulière. Voir l' aide sur evalm  pour une présentation de cette notation particulière ( evalm  : eval uate m atrix...). Effectuer le produit des deux matrices définies en 1.

>

>

3.  Vérifier que la même syntaxe permet à Maple  de calculer les puissances et les inverses de matrices.

>

>

4.  Dans cette question on se propose de reproduire "à la main" le produit de deux matrices. Construire une procédure prodmat  prenant comme argument deux matrices et retournant leur produit. On pourra utiliser rowdim et coldim  (également dans la bibliothèque linalg ) pour déterminer leurs dimensions.

>

>

II.  Matrices magiques

  Une matrice carrée est dite semi-magique  si la somme des termes de ses lignes et de ses colonnes est constante. Elle est dite magique  si cette constante est en outre égale à la somme des termes des diagonales de la matrice. On ne considérera que des matrices à coefficients entiers consécutifs   p , , ...,  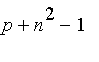si n est la taille de la matrice.

1.  Dire pourquoi on peut supposer, sans perte de généralité, que la matrice contient  entiers consécutifs à partir de 1 . Combien vaut alors la somme  des termes des lignes ou colonnes d'une matrice semi-magique ?

2.  Ecrire une procédure permettant de tester si une matrice de taille quelconque est magique. Tester sur la matrice   M  suivante :

  .

>

>

3.  Que peut-on dire du produit de deux matrices semi-magiques ? De deux matrices magiques ? (Utiliser p. ex. .)

>

>