module_suites.mws
Informatique
Suites
I. Détermination de la valeur approchée d'une limite
On définit la suite (
![u[n]](graphics/module_suites1.gif) ) pour
n
> 0 par :
) pour
n
> 0 par :
![u[n] = sqrt(1+sqrt(2+`...`+sqrt(n-1+sqrt(n))))](graphics/module_suites2.gif)
On a prouvé en exercice que cette suite est croissante et convergente, mais sans savoir calculer sa limite. On se propose de déterminer en Maple une valeur approchée de celle-ci.
1.
Définissez cette suite en Maple. (Attention, on ne cherchera pas à calculer
![u[n]](graphics/module_suites3.gif) en fonction
de
en fonction
de
![u[n-1]](graphics/module_suites4.gif) .)
.)
2.
Testez votre définition. Celle-ci doit faire apparaître l'empilement de radicaux qui compose
![u[n]](graphics/module_suites5.gif) .
.
3.
Pour les calculs numériques, introduisez dans votre définition de
![u[n]](graphics/module_suites6.gif) une approximation (
evalf
) après chaque étape du calcul (càd, chaque
une approximation (
evalf
) après chaque étape du calcul (càd, chaque
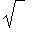 ).
).
4.
Calculer
![u[10]](graphics/module_suites8.gif) ,
,
![u[100]](graphics/module_suites9.gif) ,
,
![u[1000]](graphics/module_suites10.gif) . Que peut-on conjecturer ?
. Que peut-on conjecturer ?
II. Suite récurrente
Il s'agit d'étudier la suite définie
![u[0] = 2](graphics/module_suites11.gif) et par la relation de récurrence :
et par la relation de récurrence :
![u[n+1] = sqrt((-1)^n+u[n])](graphics/module_suites12.gif)
1.
Programmer le calcul d'un terme de la suite d'indice quelconque. Tester.
2.
Calculer
![u[n]](graphics/module_suites13.gif) pour
n
Î
[100,105] et commenter le résultat obtenu.
pour
n
Î
[100,105] et commenter le résultat obtenu.
3.
Définir en Maple les fonctions
g
et
h
faisant passer de
![u[2*n]](graphics/module_suites14.gif) à
à
![u[2*n+2]](graphics/module_suites15.gif) et de
et de
![u[2*n+1]](graphics/module_suites16.gif) à
à
![u[2*n+3]](graphics/module_suites17.gif) respectivement. Les représenter graphiquement (avec la droite d'équation
respectivement. Les représenter graphiquement (avec la droite d'équation
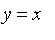 sur le même schéma). Chercher des valeurs (au moins approchées, si possible exactes) des
points fixes
de ces fonctions.
sur le même schéma). Chercher des valeurs (au moins approchées, si possible exactes) des
points fixes
de ces fonctions.
III. Visualisaton des suites récurrentes
Pour une suite récurrente
![u[n+1] = f(u[n])](graphics/module_suites19.gif) telle que
telle que
![u[n+1] = sqrt(2+u[n])](graphics/module_suites20.gif) ou encore
ou encore
![u[n+1] = 3/(2*u[n]^2+1)](graphics/module_suites21.gif) on peut visualiser les valeurs successives prises par la suite à l'aide d'un tracé en zig-zag. On souhaite faire effectuer cette représentation par Maple.
on peut visualiser les valeurs successives prises par la suite à l'aide d'un tracé en zig-zag. On souhaite faire effectuer cette représentation par Maple.
1.
Regardez dans
l'aide sur plot
quelle syntaxe permet de représenter des lignes brisées.
2.
Dans chacun des exemples ci-dessus, construisez la structure qu'il faut fournir à
plot
comme argument, pour représenter les 20 (p. ex.) premiers termes de la suite (
![u[n]](graphics/module_suites22.gif) ).
).
3.
Représentez alors ces termes sur le même schéma que la fonction
f
. (Pour cela, utilisez la fonction
display
qui nécessite au préalable une instruction
with(plots):
.)
IV. Moyenne arithmético-géométrique
Etant donnés deux nombres positifs
a
et
b
on définit les suites (
![u[n]](graphics/module_suites23.gif) ) et (
) et (
![v[n]](graphics/module_suites24.gif) ) par :
) par :
![u[0] = a](graphics/module_suites25.gif) ,
,
![v[0] = b](graphics/module_suites26.gif) et :
et :
![u[n+1] = (u[n]+v[n])/2, v[n+1] = sqrt(u[n]*v[n])](graphics/module_suites27.gif)
On montre en exercice que les suites (
![u[n]](graphics/module_suites28.gif) ) et (
) et (
![v[n]](graphics/module_suites29.gif) ) sont convergentes vers une même limite notée
) sont convergentes vers une même limite notée
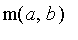 :
moyenne arithmético-géométrique
de
a
et
b.
:
moyenne arithmético-géométrique
de
a
et
b.
1.
Programmez le calcul (simultané) de
![u[n]](graphics/module_suites31.gif) et
et
![v[n]](graphics/module_suites32.gif) en fonction de
n
. On utilisera pour cela une procédure (
proc(a,b,n)
) prenant
a
,
b
et
n
comme arguments. Testez.
en fonction de
n
. On utilisera pour cela une procédure (
proc(a,b,n)
) prenant
a
,
b
et
n
comme arguments. Testez.
2.
Perfectionnez votre procédure pour en faire une autre,
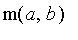 , qui s'arrête automatiquement lorsque
, qui s'arrête automatiquement lorsque
![abs(u[n]-v[n]) < 10^(-10)](graphics/module_suites34.gif) . Testez.
. Testez.
3.
Pour différentes valeurs de
a
fixées :
(a)
Définissez
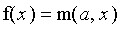 ainsi que
ainsi que
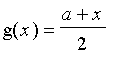 et
et
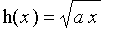 (les moyennes usuelles).
(les moyennes usuelles).
(b)
Tracez sur un même schéma les courbes de f, g et h. Quelle remarque peut-on faire ?
![]() ) pour
n
> 0 par :
) pour
n
> 0 par :
![u[n] = sqrt(1+sqrt(2+`...`+sqrt(n-1+sqrt(n))))](graphics/module_suites2.gif)
![]() en fonction
de
en fonction
de
![]() .)
.)
![]() .
.
![]() une approximation (
evalf
) après chaque étape du calcul (càd, chaque
une approximation (
evalf
) après chaque étape du calcul (càd, chaque
![]() ).
).
![]() ,
,
![]() ,
,
![]() . Que peut-on conjecturer ?
. Que peut-on conjecturer ?
![u[n+1] = sqrt((-1)^n+u[n])](graphics/module_suites12.gif)
![u[n+1] = 3/(2*u[n]^2+1)](graphics/module_suites21.gif) on peut visualiser les valeurs successives prises par la suite à l'aide d'un tracé en zig-zag. On souhaite faire effectuer cette représentation par Maple.
on peut visualiser les valeurs successives prises par la suite à l'aide d'un tracé en zig-zag. On souhaite faire effectuer cette représentation par Maple.
![u[n+1] = (u[n]+v[n])/2, v[n+1] = sqrt(u[n]*v[n])](graphics/module_suites27.gif)
![abs(u[n]-v[n]) < 10^(-10)](graphics/module_suites34.gif) . Testez.
. Testez.
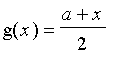 et
et